Biography
I am a researcher at Inria in POEMS team. My research focuses on wave propagation problems, Decomposition Domain Methods (DDM) and Boundary Integral Equations (BIE). I am also developing a library for distributed compressed matrices called Htool using MPI. It can be used via FreeFEM for solving BIEs, via PETSc for black-box compression, and directly via C++ or its Python interface.
I also teach at ENSTA courses related to applied mathematics and programming. I wrote Computer Tools to introduce useful tools for programming.
Previously, I was a postdoctoral researcher at the University of Bath, where I worked with Euan Spence. I did my Ph.D under the supervision of Xavier Claeys and Frédéric Nataf at Laboratoire Jacques-Louis Lions (LJLL) in Sorbonne Université, and I was a member of the joint Inria-LJLL project team Alpines. My thesis was funded by the ANR (French National Research Agency) via the ANR project NonlocalDD.
- Wave propagation problems
- Domain Decomposition Methods
- Boundary Integral Equations
- Numerical analysis
- Scientific Computing
- Computer tools
PhD in applied mathematics, 2020
Sorbonne Université
Master's degree in applied mathematics, 2016
Sorbonne Université
Engineer's degree, 2016
École Nationale des Ponts et Chaussées
Recent Publications
Other talks
Projects
Asciinema automation
Python package to automate asciinema recordings

Computer tools
Computer tools for mathematicians and computer scientists

ElastoPhi
Research project conducted during the summer school CEMRACS in 2016
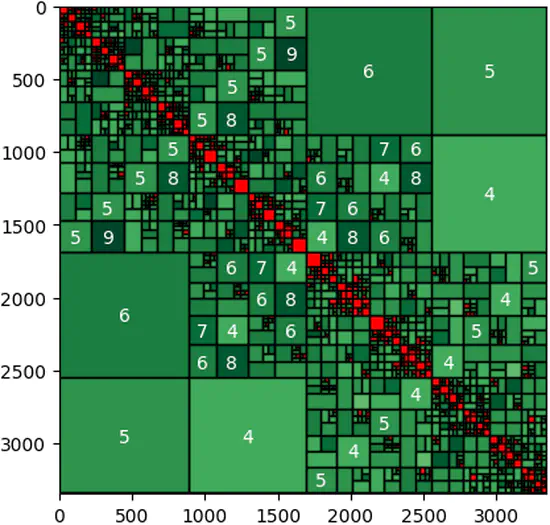
Htool
Library for parallel solvers and hierarchical matrices
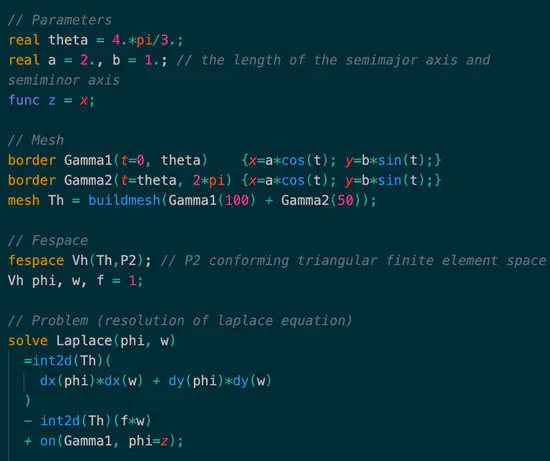
vscode-FreeFEM
vscode extension for FreeFEM
Events
A francophone young researchers conference on the numerical simulation of wave propagation (website).
- 3ème rencontre Jeunes Chercheuses Jeunes Chercheurs (JCJC) autour de la simulation numérique de la propagation d’onde
- 14 speakers, around 15 participants
- Funded by FMJH-LMH, Mission Jeunes Chercheurs Inria, SMAI (BOUM)
Supervision
Current students
- Antonin Boisneault
- PhD student (Oct. 2023 -)
- Master’s degree research internship (Apr. - Aug. 2023)
- Timothée Raynaud
- PhD student (Oct. 2023 -)
- Master’s degree research internship (Apr. - Aug. 2023)
Teaching
2023-2024
- Cours accéléré de programmation [O12] in master AMS
18 hours - slides - Programmation scientifique en C++ [SIM201] at ENSTA
14 hours – lecturer: Eric Lunéville - Programmation scientifique en C++ [SIM202] at ENSTA
21 hours – lecturer: Eric Lunéville - Introduction to Matlab [MO102]
only organisation – with Eric Lunéville
2022-2023
- Cours accéléré de programmation [O12] in master AMS
18 hours - slides - La méthode des éléments finis [ANN201] at ENSTA
15 hours – lecturer: Sonia Fliss - Programmation scientifique en C++ [SIM201] at ENSTA
14 hours – lecturer: Eric Lunéville - Programmation scientifique en C++ [SIM202] at ENSTA
21 hours – lecturer: Eric Lunéville - Introduction to Matlab [MO102]
only organisation – with Eric Lunéville
2021-2022 at ENSTA
- Introduction to Matlab [MO102]
14 hours – lecturers: Pierre Carpentier, David Filliat and Eric Lunéville - Quadratic optimization [AO101]
20 hours – lecturers: Benjamin Bonrepeaux and Wim Van Ackooij
2017-2018 at Université Pierre et Marie Curie
- M1 : Calcul scientifique pour les grands systèmes linéaires [4M053]
36 hours – lecturers: Xavier Claeys and Cindy Guichard - M1 : Mise en oeuvre de la méthode des éléments finis [4M054]
36 hours – lecturers: Xavier Claeys and Cindy Guichard
2016-2017 at Université Pierre et Marie Curie
- M1 : Calcul scientifique pour les grands systèmes linéaires [4M053]
36 hours – lecturer: Xavier Claeys - M1 : Mise en oeuvre de la méthode des éléments finis [4M054]
36 hours – lecturer: Xavier Claeys
Contact
-
828 Boulevard des Maréchaux
91120 Palaiseau